Decreased degree of hyperbolic sinus. Reference data on hyperbolic functions - properties, graphs, formulas. Formulas for the sum and difference of hyperbolic functions
Along with the connection between trigonometric and exponential functions(Euler formulas)
in the complex domain there is such a very simple connection between trigonometric and hyperbolic functions.
Recall that, according to the definition:

If in identity (3) we make a replacement with then on the right side, we get the same expression that is on the right side of the identity, from which the equality of the left sides follows. The same holds for identities (4) and (2).
![]()
By dividing both parts of identity (6) into the corresponding parts of identity (5) and, conversely, (5) by (6), we obtain:

A similar substitution in identities (1) and (2) and comparison with identities (3) and (4) give:

Finally, from identities (9) and (10) we find:

If in identities (5)-(12) we put where x - real number, i.e., consider the argument to be purely imaginary, then we obtain eight more identities between the trigonometric functions of the purely imaginary argument and the corresponding hyperbolic functions of the real argument, as well as between the hyperbolic functions of the purely imaginary Argument and the corresponding trigonometric functions of the real argument:

The resulting relations make it possible to move from trigonometric functions to hyperbolic ones and from
hyperbolic functions to trigonometric ones with the replacement of the imaginary argument by a real one. They can be formulated as the following rule:
To move from trigonometric functions of the imaginary argument to hyperbolic ones or, conversely, from hyperbolic functions of the imaginary argument to trigonometric ones, the imaginary unit of the sine and tangent should be taken out of the sign of the function, and for the cosine it should be discarded altogether.
The established connection is remarkable, in particular, in that it allows us to obtain all relations between hyperbolic functions from the known relations between trigonometric functions by replacing the latter with hyperbolic functions
Let's show you how it is. is being done.
Let us take for example the basic trigonometric identity
and put in it where x is a real number; we get:
If in this identity we replace sine and cosine with hyperbolic sine and cosine according to the formulas, then we get or and this is the main identity between previously derived in a different way.
In a similar way, you can derive all other formulas, including formulas for hyperbolic functions of the sum and difference of arguments, double and half arguments, etc., thus obtaining “hyperbolic trigonometry” from ordinary trigonometry.
Tangent, cotangent
Definitions of hyperbolic functions, their domains of definitions and values
sh x- hyperbolic sine, -∞ < x < +∞; -∞ < y < +∞ .
ch x- hyperbolic cosine
, -∞ < x < +∞; 1 ≤ y< +∞ .
th x- hyperbolic tangent
, -∞ < x < +∞; - 1 < y < +1 .
cth x- hyperbolic cotangent
, x ≠ 0 ; y< -1 или y > +1 .
Graphs of hyperbolic functions
Hyperbolic sine graph y = sh x

Graph of hyperbolic cosine y = ch x

Graph of hyperbolic tangent y = th x

Graph of hyperbolic cotangent y = cth x
Formulas with hyperbolic functions
Connection with trigonometric functions
sin iz = i sh z ; cos iz = ch z
sh iz = i sin z; ch iz = cos z
tg iz = i th z ; cot iz = - i cth z
th iz = i tg z ; cth iz = - i cot z
Here i is the imaginary unit, i 2 = - 1
.
Applying these formulas to trigonometric functions, we obtain formulas connecting hyperbolic functions.
Parity
sh(-x) = - sh x;
ch(-x) = ch x.
th(-x) = - th x;
cth(-x) = - cth x.
Function ch(x)- even. Functions sh(x), th(x), cth(x)- odd.
Difference of squares
ch 2 x - sh 2 x = 1.
Formulas for the sum and difference of arguments
sh(x y) = sh x ch y ch x sh y,
ch(x y) = ch x ch y sh x sh y,
,
,
sh 2 x = 2 sh x ch x,
ch 2 x = ch 2 x + sh 2 x = 2 ch 2 x - 1 = 1 + 2 sh 2 x,
.
Formulas for the products of hyperbolic sine and cosine
,
,
,
,
,
.
Formulas for the sum and difference of hyperbolic functions
,
,
,
,
.
Relation of hyperbolic sine and cosine with tangent and cotangent
,
,
,
.
Derivatives
,
Integrals of sh x, ch x, th x, cth x
,
,
.
Series expansions
Inverse functions
Areasinus
At - ∞< x < ∞
и - ∞ < y < ∞
имеют место формулы:
,
.
Areacosine
At 1 ≤ x< ∞
And 0 ≤ y< ∞
the following formulas apply:
,
.
The second branch of the areacosine is located at 1 ≤ x< ∞
and - ∞< y ≤ 0
:
.
Areatangent
At - 1
< x < 1
and - ∞< y < ∞
имеют место формулы:
,
11 Basic functions of a complex variable
Let us recall the definition of a complex exponent – . Then
Maclaurin series expansion. The radius of convergence of this series is +∞, which means that the complex exponential is analytic on the entire complex plane and
(exp z)"=exp z; exp 0=1. (2)
The first equality here follows, for example, from the theorem on term-by-term differentiation of a power series.
11.1 Trigonometric and hyperbolic functions
Sine of a complex variable called function

Cosine of a complex variable there is a function

Hyperbolic sine of a complex variable is defined like this:
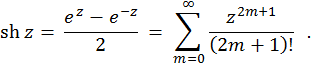
Hyperbolic cosine of a complex variable-- this is a function

Let us note some properties of the newly introduced functions.
A. If x∈ ℝ, then cos x, sin x, cosh x, sh x∈ ℝ.
B. The following connection exists between trigonometric and hyperbolic functions:
cos iz=ch z; sin iz=ish z, ch iz=cos z; sh iz=isin z.
B. Basic trigonometric and hyperbolic identities:
cos 2 z+sin 2 z=1; ch 2 z-sh 2 z=1.
Proof of the main hyperbolic identity.
The main trigonometric identity follows from the main hyperbolic identity when taking into account the connection between trigonometric and hyperbolic functions (see property B)
G Addition formulas:
In particular,
D. To calculate the derivatives of trigonometric and hyperbolic functions, one should apply the theorem on term-by-term differentiation of a power series. We get:
(cos z)"=-sin z; (sin z)"=cos z; (ch z)"=sh z; (sh z)"=ch z.
E. The functions cos z, ch z are even, and the functions sin z, sin z are odd.
J. (Frequency) The function e z is periodic with period 2π i. The functions cos z, sin z are periodic with a period of 2π, and the functions ch z, sin z are periodic with a period of 2πi. Moreover,
Applying the sum formulas, we get
Z. Expansion into real and imaginary parts:
If a single-valued analytic function f(z) bijectively maps a domain D onto a domain G, then D is called a univalent domain.
AND. Region D k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Proof. From relation (5) it follows that the mapping exp:D k → ℂ is injective. Let w be any non-zero complex number. Then, solving the equations e x =|w| and e iy =w/|w| with real variables x and y (y is chosen from the half-interval)
