I will solve the exam derivative. Functions. Main types, schedules, methods of assignment. Graphical method of constructing a function

In task No. 13 of the Unified State Examination in mathematics basic level You will have to demonstrate skills and knowledge of one of the concepts of the behavior of a function: derivatives at a point or rates of increase or decrease. The theory for this task will be added a little later, but this will not prevent us from examining in detail several typical options.

Analysis of typical options for tasks No. 14 of the Unified State Exam in basic level mathematics

Option 14MB1

The graph shows the dependence of temperature on time during the heating process of a passenger car engine. The horizontal axis shows the time in minutes that has passed since the engine started; on the vertical axis is the engine temperature in degrees Celsius.

Using the graph, match each time interval with the characteristics of the engine heating process during this interval.

In the table, under each letter, indicate the corresponding number.

Execution algorithm:

1. Select the time interval during which the temperature dropped.
2. Apply a ruler to 30°C and determine the time interval during which the temperature was below 30°C.

Solution:

Let us choose the time interval during which the temperature dropped. This section is visible to the naked eye; it begins 8 minutes from the moment the engine starts.

Apply a ruler to 30°C and determine the time interval during which the temperature was below 30°C.

Below the ruler there will be a section corresponding to the time interval 0 - 1 min.

Using a pencil and a ruler, we will find at what time interval the temperature was in the range from 40°C to 80°C.

Let us drop perpendiculars from the points corresponding to 40°С and 80°С onto the graph, and from the resulting points we lower the perpendiculars onto the time axis.

We see that this temperature interval corresponds to a time interval of 3 – 6.5 minutes. That is, from those given in the condition 3 – 6 minutes.

Using the method of elimination, we will select the missing answer option.

Option 14MB2

Solution:

Let's analyze the graph of function A. If the function increases, then the derivative is positive and vice versa. The derivative of the function is equal to zero at the extremum points.

First, function A increases, i.e. the derivative is positive. This corresponds to the graphs of derivatives 2 and 3. At the maximum point of the function x = -2, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 3.

First, function B decreases, i.e. the derivative is negative. This corresponds to the graphs of derivatives 1 and 4. The maximum point of the function is x=-2, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 4.

First, function B increases, i.e. the derivative is positive. This corresponds to the graphs of derivatives 2 and 3. The maximum point of the function is x = 1, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 2.

Using the method of elimination, we can determine that the graph of the function Г corresponds to the graph of the derivative numbered 1.

Answer: 3421.

Option 14MB3

Execution algorithm for each function:

1. Determine the intervals of increasing and decreasing functions.
2. Determine the maximum and minimum points of functions.
3. Draw conclusions and match the proposed graphs.

Solution:

Let's analyze the graph of function A.

If the function is increasing, then the derivative is positive and vice versa. The derivative of the function is equal to zero at the extremum points.

The extremum point is the point at which the maximum or minimum value of the function is reached.

First, function A increases, i.e. the derivative is positive. This corresponds to the graphs of derivatives 3 and 4. At the maximum point of the function x=0, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 4.

Let's analyze the graph of function B.

First, function B decreases, i.e. the derivative is negative. This corresponds to the graphs of derivatives 1 and 2. The minimum point of the function is x=-1, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 2.

Let's analyze the graph of function B.

First, function B decreases, i.e. the derivative is negative. This corresponds to the graphs of derivatives 1 and 2. The minimum point of the function is x = 0, that is, at this point the derivative should be equal to zero. This condition corresponds to graph number 1.

Using the method of elimination, we can determine that the graph of the function Г corresponds to the graph of the derivative numbered 3.

Answer: 4213.

Option 14MB4

The figure shows the graph of the function and the tangents drawn to it at the abscissa points A, B, C and D.The right column shows the values ​​of the derivative at points A, B, C and D. Using the graph, match each point with the value of the derivative of the function at it.

POINTS
A
IN
WITH
D

DERIVATIVE VALUES
1) –4
2) 3
3) 2/3
4) -1/2

Let's remember what the derivative means, namely its value at a point - the value of the derivative function at a point is equal to the tangent of the angle of inclination (coefficient) of the tangent.

In the answers we have two positive and two negative options. As we remember, if the coefficient is straight (graphics y = kx+ b) is positive, then the line increases, but if it is negative, then the line decreases.

We have two increasing lines - at points A and D. Now let's remember what the value of the coefficient k means?

The coefficient k shows how quickly the function increases or decreases (in fact, the coefficient k is itself a derivative of the function y = kx+ b).

Therefore, k = 2/3 corresponds to a flatter straight line - D, and k = 3 - A.

The same is true in the case of negative values: point B corresponds to a steeper straight line with k = - 4, and point C - -1/2.

Option 14MB5

The dots in the figure show the monthly sales volumes of heaters in a household appliance store. The months are indicated horizontally, and the number of heaters sold vertically. For clarity, the points are connected by a line.

Using the figure, match each of the indicated time periods with the characteristics of heater sales.

Execution algorithm

We analyze the parts of the graph corresponding different times of the year. We formulate the situations shown on the graph. We find the most suitable answers for them.

Solution:

In winter, the number of sales exceeded 120 units/month, and it was increasing all the time. This situation corresponds to answer option No. 3. Those. we get: A–3.

In the spring, sales gradually fell from 120 heaters per month to 50. The closest to this formulation is option No. 2. We have: B–2.

In summer, the number of sales did not change and was minimal. The 2nd part of this formulation is not reflected in the answers, and only No. 4 is suitable for the first. From here we have: AT 4.

In the fall, sales grew, but their number in no month exceeded 100 units. This situation is described in option No. 1. We get: G–1.

Option 14MB6

The graph shows the dependence of the speed of a regular bus on time. The vertical axis shows the speed of the bus in km/h, and the horizontal axis shows the time in minutes since the bus started moving.

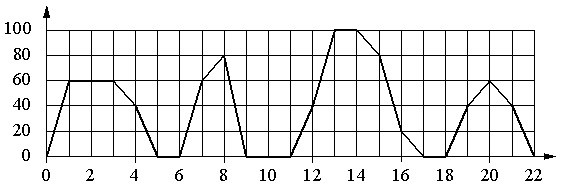
Using the graph, match each time interval with the characteristics of the bus movement during this interval.

Execution algorithm

1. We determine the division price on the horizontal and vertical scales.
2. We analyze in turn the proposed statements 1–4 from the right column (“Characteristics”). We compare them with time intervals from the left column of the table and find “letter-number” pairs for the answer.

Solution:

The horizontal scale division is 1 s, the vertical scale is 20 km/h.

1. When the bus makes a stop, its speed is 0. The bus had zero speed for 2 minutes in a row only from the 9th to the 11th minute. This time falls within the range of 8–12 minutes. So, we have a couple for the answer: B–1.
2. The bus had a speed of 20 km/h or more for several periods of time. Moreover, option A is not suitable here, because, for example, in the 7th minute the speed was 60 km/h, option B - because it has already been applied, option D - because at the beginning and end of the interval the bus had zero speed . In this case, option B (12–16 min) is suitable; During this interval, the bus starts moving at a speed of 40 km/h, then accelerates to 100 km/m and then gradually reduces the speed to 20 km/h. So we have: AT 2.
3. There is a speed limit here. At the same time, we do not consider options B and C. The remaining intervals A and D are both suitable. Therefore, it would be correct to consider the 4th option first, and then return to the 3rd.
4. Of the two remaining intervals, only 4–8 minutes are suitable for characteristic No. 4, since there was a stop during this interval (at the 6th minute). There were no stops between 18 and 22 minutes. We get: A–4. It follows that for characteristic No. 3 you need to take the interval Г, i.e. it turns out to be a couple G–3.

Option 14MB7

The dots in the figure show China's population growth between 2004 and 2013. The horizontal line indicates the year, the vertical line indicates population growth as a percentage (increase in population relative to the previous year). For clarity, the points are connected by a line.

Using the figure, match each of the indicated time periods with the characteristics of China's population growth during this period.

Execution algorithm

1. We determine the price of dividing the vertical scale of the drawing. It is found as the difference between a pair of adjacent scale values, divided by 2 (since there are 2 divisions between two adjacent values).
2. We analyze sequentially the characteristics 1–4 given in the condition (left table column). We compare each of them with a specific period of time (right table column).

Solution:

The vertical scale division value is 0.01%.

1. The decline in growth continued continuously from 2004 to 2010. In 2010–2011, the increase was consistently minimal, and starting in 2012 it began to increase. Those. growth stopped in 2010. This year is in the period 2009–2011. Accordingly, we have: IN 1.
2. The largest drop in growth should be considered the “steepest” falling line of the graph in the figure. It falls on the period 2006–2007. and is 0.04% per year (0.59–0.56=0.04% in 2006 and 0.56–0.52=0.04% in 2007). From here we get: A–2.
3. The growth indicated in characteristic No. 3 began in 2007, continued in 2008 and ended in 2009. This corresponds to time period B, i.e. we have: B–3.
4. Population growth began to increase after 2011, i.e. in 2012–2013 Therefore we get: G–4.

Option 14MB8

The figure shows the graph of the function and the tangents drawn to it at points with abscissas A, B, C and D.

The right column shows the values ​​of the derivative of the function at points A, B, C and D. Using the graph, match each point with the value of the derivative of the function at it.

Execution algorithm

1. We consider a pair of tangents having sharp corner with the positive direction of the abscissa axis. We compare them and find a match among the pair of corresponding derivative values.
2. We consider a pair of tangents forming the x-axis in the positive direction obtuse angle. We compare them modulo and determine their correspondence to the values ​​of the derivatives among the two remaining ones in the right column.

Solution:

An acute angle with the positive direction of the abscissa axis is formed by derivatives in T.B and T.S. These derivatives have positive values. Therefore, here you should choose between values ​​No. 1 and 3. Applying the rule that if the angle is less than 45 0, then the derivative is less than 1, and if it is more, then it is more than 1, we conclude: in point B, the modulo derivative is greater than 1, in t.C – less than 1. This means that you can make pairs for the answer: AT 3 And S–1.

The derivatives in t.A and t.D form an obtuse angle with the positive direction of the abscissa axis. And here we apply the same rule, paraphrasing it a little: the more the tangent at a point is “pressed” to the line of the x-axis (towards its negative direction), the greater its modulus. Then we get: the derivative in t.A is less in absolute value than the derivative in t.D. From here we have pairs for the answer: A–2 And D–4.

Option 14MB9

The dots in the figure show the average daily air temperature in Moscow in January 2011. The dates of the month are indicated horizontally, and the temperature in degrees Celsius is indicated vertically. For clarity, the points are connected by a line.

Using the figure, match each of the indicated time periods with the characteristic of temperature change.

Execution algorithm

We analyze characteristics 1–4 (right column) sequentially, using the graph in the figure. We assign each of them to a specific time period (left column).

Solution:

1. An increase in temperature was observed only at the end of the period January 22–28. Here, on the 27th and 28th, it increased by 1 and 2 degrees, respectively. At the end of the period January 1–7, the temperature was stable (–10 degrees); at the end of January 8–14 and 15–21 it decreased (from –1 to –2 and from –11 to –12 degrees, respectively). Therefore we get: G–1.
2. Since each time period covers 7 days, the temperature needs to be analyzed starting from the 4th day of each period. The temperature remained constant for 3–4 days only from January 4 to January 7. Therefore we get the answer: A–2.
3. The monthly minimum temperature was observed on January 17. This number falls within the period January 15–21. From here we have a pair: AT 3.
4. The temperature maximum occurred on January 10 and was +1 degree. This date falls between January 8–14. So we have: B–4.

Option 14MB10

Execution algorithm

1. The value of the function at a point is positive if this point is located above the Ox axis.
2. The derivative at a point is greater than zero if the tangent to this point forms an acute angle with the positive direction of the Ox axis.

Solution:

Point A. It is located below the Ox axis, which means the value of the function in it is negative. If you draw a tangent in it, then the angle between it and the positive direction Ox will be about 90 0, i.e. forms an acute angle. This means that characteristic No. 3 is suitable in this case. Those. we have: A–3.

Point B. It is located above the Ox axis, i.e. the point has a positive value of the function. The tangent at this point will be quite close to the x-axis, forming an obtuse angle (slightly less than 180 0) with its positive direction. Accordingly, the derivative at this point is negative. Thus, characteristic 1 is suitable here. We get the answer: IN 1.

Point C. The point is located below the Ox axis, the tangent at it forms a large obtuse angle with the positive direction of the x-axis. Those. in t.C the value of both the function and the derivative is negative, which corresponds to characteristic No. 2. Answer: S–2.

Point D. The point is located above the Ox axis, and the tangent at it forms an acute angle with the positive direction of the axis. This suggests that both the value of the function and the value of the derivative here are greater than zero. Answer: D–4.

Option 14MB11

The dots in the figure show the monthly sales volumes of refrigerators in a household appliance store. The months are indicated horizontally, and the number of refrigerators sold vertically. For clarity, the points are connected by a line.

Using the figure, match each of the indicated time periods with the characteristics of refrigerator sales.

Sergey Nikiforov

If the derivative of a function is of constant sign on an interval, and the function itself is continuous on its boundaries, then the boundary points are added to both increasing and decreasing intervals, which fully corresponds to the definition of increasing and decreasing functions.

Farit Yamaev 26.10.2016 18:50

Hello. How (on what basis) can we say that at the point where the derivative is equal to zero, the function increases. Give reasons. Otherwise, it's just someone's whim. By what theorem? And also proof. Thank you.

Support

The value of the derivative at a point is not directly related to the increase in the function over the interval. Consider, for example, functions - they are all increasing on the interval

Vladlen Pisarev 02.11.2016 22:21

If a function is increasing on the interval (a;b) and is defined and continuous at points a and b, then it is increasing on the interval . Those. point x=2 is included in this interval.

Although, as a rule, increase and decrease are considered not on a segment, but on an interval.

But at the point x=2 itself, the function has a local minimum. And how to explain to children that when they are looking for points of increase (decrease), we do not count the points of local extremum, but enter into intervals of increase (decrease).

Considering that the first part of the Unified State Exam For " middle group kindergarten", then perhaps such nuances are too much.

Separately, many thanks to all the staff for “Solving the Unified State Exam” - an excellent guide.

Sergey Nikiforov

A simple explanation can be obtained if we start from the definition of an increasing/decreasing function. Let me remind you that it sounds like this: a function is called increasing/decreasing on an interval if a larger argument of the function corresponds to a larger/smaller value of the function. This definition does not use the concept of derivative in any way, so questions about the points where the derivative vanishes cannot arise.

Irina Ishmakova 20.11.2017 11:46

Good afternoon. Here in the comments I see beliefs that boundaries need to be included. Let's say I agree with this. But please look at your solution to problem 7089. There, when specifying increasing intervals, boundaries are not included. And this affects the answer. Those. the solutions to tasks 6429 and 7089 contradict each other. Please clarify this situation.

Alexander Ivanov

Tasks 6429 and 7089 have completely different questions.

One is about increasing intervals, and the other is about intervals with a positive derivative.

There is no contradiction.

The extrema are included in the intervals of increasing and decreasing, but the points in which the derivative is equal to zero are not included in the intervals in which the derivative is positive.

A Z 28.01.2019 19:09

Colleagues, there is a concept of increasing at a point

(see Fichtenholtz for example)

and your understanding of the increase at x=2 is contrary to the classical definition.

Increasing and decreasing is a process and I would like to adhere to this principle.

In any interval that contains the point x=2, the function is not increasing. Therefore inclusion given point x=2 is a special process.

Usually, to avoid confusion, inclusion of the ends of intervals is discussed separately.

Alexander Ivanov

A function y=f(x) is said to be increasing over a certain interval if a larger value of the argument from this interval corresponds to a larger value of the function.

At the point x=2 the function is differentiable, and on the interval (2; 6) the derivative is positive, which means on the interval .

Show solution

Solution

The graph shows that the derivative f"(x) of the function f(x) changes sign from plus to minus (at such points there will be a maximum) at exactly one point (between -5 and -4) from the interval [-6; -2 ] Therefore, there is exactly one maximum point in the interval [-6; -2].

Answer

Source: “Mathematics. Preparation for the Unified State Exam 2017. Profile level." Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

The figure shows a graph of the function y=f(x), defined on the interval (-2; 8).

Show solution

Solution

Determine the number of points at which the derivative of the function f(x) is equal to 0.

Answer

Source: “Mathematics. Preparation for the Unified State Exam 2017. Profile level." Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

The equality of the derivative at a point to zero means that the tangent to the graph of the function drawn at this point is parallel to the Ox axis.

Show solution

Solution

Therefore, we find points at which the tangent to the graph of the function is parallel to the Ox axis.

On this chart, such points are extremum points (maximum or minimum points). As you can see, there are 5 extremum points.

Answer

Source: “Mathematics. Preparation for the Unified State Exam 2017. Profile level." Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

The figure shows a graph of the function y=f(x) and points -6, -1, 1, 4 are marked on the abscissa. At which of these points is the derivative the smallest? Please indicate this point in your answer.

Back forward

Attention! Slide previews are for informational purposes only and may not represent all the features of the presentation. If you are interested in this work, please download the full version.

Lesson type: repetition and generalization.

Lesson format: lesson-consultation.

Lesson objectives:

• educational: repeat and generalize theoretical knowledge on the topics: “Geometric meaning of the derivative” and “Application of the derivative to the study of functions”; consider all types of B8 problems encountered on the Unified State Examination in mathematics;
• provide students with the opportunity to test their knowledge by solving problems independently; teach how to fill out the exam answer form;
• developing: to promote the development of communication as a method of scientific knowledge, semantic memory and voluntary attention; the formation of such key competencies as comparison, juxtaposition, classification of objects, determination of adequate ways to solve an educational task based on given algorithms, the ability to act independently in situations of uncertainty, monitor and evaluate one’s activities, find and eliminate the causes of difficulties;

educational

: develop students’ communicative competencies (communication culture, ability to work in groups); promote the development of the need for self-education. Technologies: developmental education, ICT.

Teaching methods: verbal, visual, practical, problematic.

Forms of work:

individual, frontal, group.

Educational and methodological support:

1. Algebra and the beginnings of mathematical analysis. 11th grade: textbook. For general education Institutions: basic and profile. levels / (Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin); edited by A. B. Zhizhchenko. – 4th ed. – M.: Education, 2011.

2. Unified State Exam: 3000 problems with answers in mathematics. All tasks of group B / A.L. Semenov, I.V. Yashchenko and others; edited by A.L. Semyonova, I.V. Yashchenko. – M.: Publishing house “Exam”, 2011. 3. Open task bank. Equipment and materials for the lesson: projector, screen, PC for each student with a presentation installed on it, printout of a memo for all students (Annex 1) .

and score sheet ( as homework, students are asked to repeat theoretical material from the textbook on the topics: “Geometric meaning of the derivative”, “Application of the derivative to the study of functions”; The class is divided into groups (4 people each), in each of which there are students of different levels.

Lesson explanation: This lesson is taught in 11th grade at the stage of repetition and preparation for the Unified State Exam. The lesson is aimed at repetition and generalization of theoretical material, at applying it to solving exam problems. Lesson duration - 1.5 hours .

This lesson is not attached to the textbook, so it can be taught while working on any teaching materials. This lesson can also be divided into two separate ones and taught as final lessons on the topics covered.

During the classes

I. Organizational moment.

II. Setting goals lesson.

III. Repetition on the topic “Geometric meaning of derivatives.”

Oral frontal work using a projector (slides No. 3-7)

Work in groups: solving problems with hints, answers, with teacher consultation (slides No. 8-17)

IV. Independent work 1.

Students work individually on a PC (slides No. 18-26), and enter their answers into the evaluation sheet. If necessary, you can consult a teacher, but in this case the student will lose 0.5 points. If the student completes the work earlier, he can choose to solve additional tasks from the collection, pp. 242, 306-324 (additional tasks are assessed separately).

V. Mutual verification.

Students exchange assessment sheets, check a friend’s work, and assign points (slide No. 27)

VI. Correction of knowledge.

VII. Repetition on the topic “Application of the derivative to the study of functions”

Oral frontal work using a projector (slides No. 28-30)

Work in groups: solving problems with hints, answers, with teacher consultation (slides No. 31-33)

VIII. Independent work 2.

Students work individually on a PC (slides No. 34-46), and enter their answers on the answer form. If necessary, you can consult a teacher, but in this case the student will lose 0.5 points. If the student completes the work earlier, he can choose to solve additional tasks from the collection, pp. 243-305 (additional tasks are assessed separately).

IX. Peer review.

Students exchange assessment sheets, check their friend’s work, and assign points (slide No. 47).

X. Correction of knowledge.

Students work again in their groups, discuss the solution, and correct mistakes.

XI. Summarizing.

Each student calculates their points and puts a grade on the score sheet.

Students submit to the teacher an assessment sheet and solutions to additional problems.

Each student receives a memo (slide No. 53-54).

XII. Reflection.

Students are asked to evaluate their knowledge by choosing one of the phrases:

• I succeeded!!!
• We need to solve a couple more examples.
• Well, who came up with this math!

XIII. Homework.

For homework, students are asked to choose tasks from the collection, pp. 242-334, as well as from an open bank of tasks.

EXTRACURRICULAR PRACTICAL WORK 2

Transformation of function graphs.

Target

Construct graphs of functions using various transformations and answer the question of the problem.

Completing of the work

Guidelines

The work is designed for 10 options, the number of the option coincides with the last digit of the serial number in the list. For example, 1, 11, 21, 31...perform option 1, 2,12, 22... - option 2, etc.

The work consists of two parts: the first part of tasks 1 - 5, these are tasks that must be completed in order to receive credit; if these tasks are completed with an error, you need to correct them and resubmit the work for verification. The second part contains tasks, by completing which you can earn an additional grade: the main part +2 tasks is “4”, the main part +3 tasks is “5”.

Task 1. The graph of a linear function is a straight line; two points are enough to construct it. (we take the values ​​of the argument x arbitrarily, and calculate the value of the function y by substituting them into the formula).

To check whether the graph of a function passes through a specified point, you need to substitute the coordinates of the point instead of x and y; if you get the correct equality, then the straight line passes through the specified point, otherwise it does not.

Task 2, 3, 4. The graphs of the indicated functions are obtained from the graphs of the functions , using a shift along the x or y axis.

, first we build a graph of the function or , then shift it by “a” units to the right or left (+a – left, -a to the right), then shift it by “b” units up or down (+b – up, -b – down)

Same with other functions:

Task 5 To graph a function: , you need to: 1) build a graph of the function , 2) the part of the graph that is located above the x-axis is left unchanged, 3) the part of the graph that is located below the x-axis is mirrored.

Problems for independent solution.

Mandatory part

Task 1. Construct a graph of a linear function, determine whether the graph of the function passes through the specified point:

Task 2. Construct a graph of a quadratic function, indicate the set of values ​​of this function.

Task 3. Construct a graph of the function, determine whether the specified function increases or decreases.

Task 4. Construct a graph of the function, answer the question of the problem.

Task 5. Construct a graph of a function containing the modulus sign.

Tasks for additional assessment.

Task 6. Plot a graph of a function specified piecewise, determine whether this function has a break point:

Task 7. Determine how many solutions the system of equations has, justify your answers. Draw conclusions by answering the questions.

What functions did you plot in this work?

What is the graph of a linear function called?

What is the graph of a quadratic function called?

What graph transformations do you know?

How is the graph of an even function located in the coordinate system? Graph of an odd function?